단계별 문제풀이 (23단계)
https://www.acmicpc.net/problem/2565
# 문제
두 전봇대 A와 B 사이에 하나 둘씩 전깃줄을 추가하다 보니 전깃줄이 서로 교차하는 경우가 발생하였다. 합선의 위험이 있어 이들 중 몇 개의 전깃줄을 없애 전깃줄이 교차하지 않도록 만들려고 한다.
예를 들어, < 그림 1 >과 같이 전깃줄이 연결되어 있는 경우 A의 1번 위치와 B의 8번 위치를 잇는 전깃줄, A의 3번 위치와 B의 9번 위치를 잇는 전깃줄, A의 4번 위치와 B의 1번 위치를 잇는 전깃줄을 없애면 남아있는 모든 전깃줄이 서로 교차하지 않게 된다.

전깃줄이 전봇대에 연결되는 위치는 전봇대 위에서부터 차례대로 번호가 매겨진다. 전깃줄의 개수와 전깃줄들이 두 전봇대에 연결되는 위치의 번호가 주어질 때, 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 구하는 프로그램을 작성하시오.
# 예제
입력 : 첫째 줄에는 두 전봇대 사이의 전깃줄의 개수가 주어진다. 전깃줄의 개수는 100 이하의 자연수이다. 둘째 줄부터 한 줄에 하나씩 전깃줄이 A전봇대와 연결되는 위치의 번호와 B전봇대와 연결되는 위치의 번호가 차례로 주어진다. 위치의 번호는 500 이하의 자연수이고, 같은 위치에 두 개 이상의 전깃줄이 연결될 수 없다.
8
1 8
3 9
2 2
4 1
6 4
10 10
9 7
7 6
출력 : 첫째 줄에 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 출력한다.
3
# 필요개념
없애야 하는 전깃줄을 세기에는 코드가 복잡해질 거 같아서 연결해도 되는 전깃줄 수를 구한 후, 전체 전깃줄 개수에서 빼주었다. 연결해도 되는 전깃줄이란, 기존 전깃줄들과 엉키지 않는 전깃줄의 개수이고, 이 개수가 최대가 되면 된다.
입력을 받을 때 무작위로 들어오기 때문에, 그대로 사용하면 시작점과 끝점을 모두 고려해 엉키는지 여부를 확인해야 하는데, 이는 너무 복잡하다고 느껴졌다. 그래서 시작점을 기준으로 오름차순 정렬하여 끝점이 기존 끝점보다 작으면 엉키는 것으로 간주해 문제를 풀었다.
초기값은 자기자신을 고려해 1로 두고, 엉키지 않는다면 이전 점의 값에 1을 더해가는 방식으로 진행했다. 애초에 N의 최대가 그리 크지 않아서 이중반복문을 사용하는데 불안함은 없었다 !
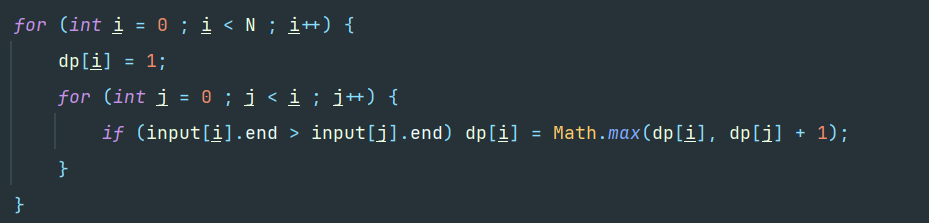
이렇게 진행한 뒤, N - dp배열의 값 중 최대값을 출력하면 되었다.
# Code
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
Node[] input = new Node[N];
int[] dp = new int[N];
for (int i = 0 ; i < N ; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
input[i] = new Node(start, end);
}
Arrays.sort(input, new Comparator<Node>() {
@Override
public int compare(Node o1, Node o2) {
return o1.start - o2.start;
}
});
for (int i = 0 ; i < N ; i++) {
dp[i] = 1;
for (int j = 0 ; j < i ; j++) {
if (input[i].end > input[j].end) dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
int max = 0;
for (int i = 0 ; i < N ; i++) {
max = Math.max(max, dp[i]);
}
System.out.println(N - max);
}
}
class Node {
int start;
int end;
public Node(int s, int e) {
this.start = s;
this.end = e;
}
}
# 결과

'코딩테스트 > 백준 골드' 카테고리의 다른 글
| [백준] 2357: 최솟값과 최댓값 (세그먼트 트리) - JAVA (0) | 2025.01.20 |
|---|---|
| [백준] 11054: 가장 긴 바이토닉 부분 수열 (DP) - JAVA (2) | 2025.01.17 |
| [백준] 2293: 동전 1 (dp) - JAVA (0) | 2025.01.10 |
| [백준] 1092: 배 (그리디 알고리즘, 정렬) - JAVA (0) | 2025.01.06 |
| [백준] 7453: 합이 0인 네 정수 (이분탐색, upper bound & lower bound) - JAVA (0) | 2024.12.28 |
