이번 챕터에서는 그래프에 대해 알아보고, 그래프를 이용해 최단거리를 구하는 Floyd algorithm (플로이드 알고리즘)도 살펴보려고 한다. 목차는 아래와 같다.
- 그래프 이론
- 플로이드 알고리즘
- 최단경로 구하기 - Floyd vs Brute-force
1. 그래프이론 (Graph Theory)
정말정말 x100!! 중요한 부분이다. 그래프 부분을 해놔야 이후에 나오는 다른 문제들을 해결할 수 있다!
그래프는 여러 개의 점(정점)들이 간선으로 연결된 구조를 나타낸다. 즉 그래프는 정점(V)와 간선(E)로 구성된다.
G = (V, E)
그래프 종류
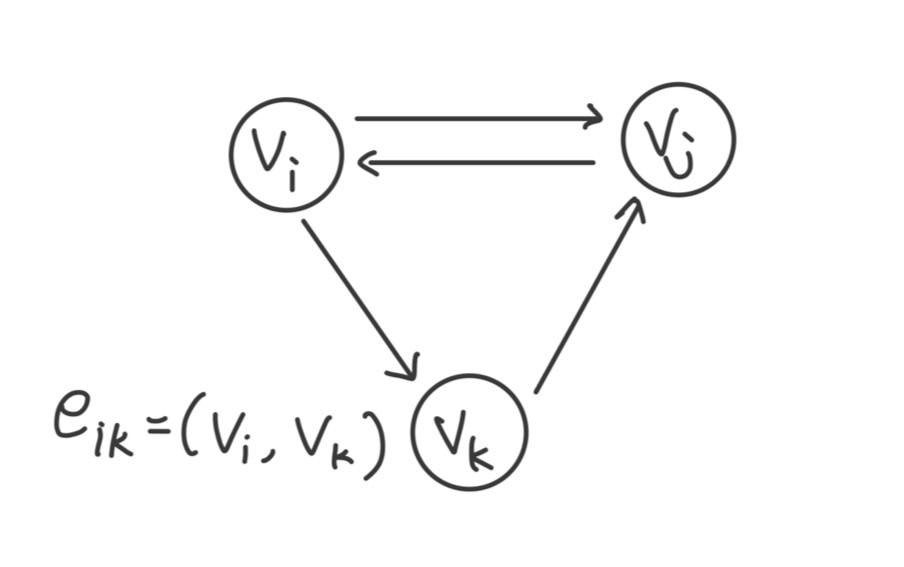
그래프는 가중치 존재의 여부, 방향 존재의 여부에 따라 종류가 다양하다.
- 가중치그래프 (weighted graph) : 간선에 값(가중치)이 존재한다면 그 그래프를 가중치그래프라고 부른다.
- 방향그래프 (directed graph) : 간선에 방향이 존재하는 경우, 예를 들면 위 그림처럼 vi에서 vj로 가는 간선과 vj에서 vi로 가는 간선이 따로 존재하는 경우, 이런 그래프를 방향그래프 (directed graph)라고 한다.
그래프 관련 용어
- 정점 (Vertex) : 데이터를 저장할 수 있는 하나의 점
- 간선 (Edge) : 정점을 연결하는 선
- 차수 (Degree) : 노드에 연결된 간선의 수
- 경로 (Path) : 그래프에서 노드에 연결된 간선의 순서를 나타내는 순서쌍
- 'path가 simple하다' 라는 표현은 같은 정점을 두 번 이상 지나지 않는 것을 의미한다. (중복x)
- 가중치그래프에서 경로의 길이는 가중치의 합이다.
- 사이클 (Cycle) : 순환형 그래프 (순환이 한개라도 존재하면 사이클)
- 가중치 (Weight) : 간선에 할당된 값
우리는 주로 가중치 그래프를 다루고, 그래프의 가중치들은 2차원 배열에 담아둔다.

해당 그래프는 아래 이차원 배열처럼 정리할 수 있다.
| 0 | 1 | ∞ | 1 | 5 |
| 9 | 0 | 3 | 2 | ∞ |
| ∞ | ∞ | 0 | 4 | ∞ |
| ∞ | ∞ | 2 | 0 | 3 |
| 3 | ∞ | ∞ | ∞ | 0 |
이렇게 가중치를 담은 이차원 배열을 W라고 칭한다. (Weight)
자기자신에서 자기자신으로 가는건 거리가 없으므로 0으로 채우고, 직항 즉 한번에 가는 길이 없으면 ∞로 채운다.
그래서 우하향 대각선은 0으로 구성되며, 무방향그래프의 경우에는 0대각선 대칭으로 값이 같게 설정된다!
2. 플로이드 알고리즘 (Floyd's algorithm)
플로이드 알고리즘은 양수 가중치 그래프에서 최단경로를 찾는 알고리즘이다.
우리에게 가중치가 들어있는 이차원 배열 W를 주고, 이를 이용해 가장 짧은 경로의 길이가 담긴 이차원 배열인 D를 반환해야한다.
이렇게 최단경로처럼 최적화된 값을 구하는 문제를 Optimization Problem 이라고 부른다!
플로이드 알고리즘은 재귀 방식을 이용한다.
D(k)[ i ][ j ] = {v1, v2, ... , vk}
k는 경유가능한 공항이라고 보면 편하다. 이 경우에는 v1부터 vk까지만 경유할 수 있고, 어디를 경유할지, 경유를 할지 말지는 최솟값인 것으로 고르면 된다. 이를 식으로 나타내면 다음과 같다.
D(k)[ i ][ j ] = min( D(k-1)[ i ][ j ], D(k-1)[ i ][ k ] + D(k-1)[ k ][ j ] )
그래서 k가 0인 경우는 중간에 다른 지점을 경유하지 않는 경우를 뜻하므로, W배열을 그대로 사용한다.
# Code
void floyd(int n, const number W[][], number D[][]) {
int i, j, k;
D = W; // D(0) = W
for (k = 1 ; k <= n ; k++) {
for (i = 1 ; i <= n ; i++) {
for (j = 1 ; j <= n ; j++) {
D[i][j] = minimum(D[i][j], D[i][k] + D[k][j]); // 경유와 직항 중 최단
}
}
}
}
# Time Complexity
이는 삼중 반복문을 사용하므로 T(n) = n * n * n = n^3 ∈ θ(n^3)
3. 최단경로 구하기 - Floyd vs Brute-force
플로이드를 이용했을 땐 n^3의 시간복잡도가 계산되었다. 여기까지만 해도 되지만, 교안에 Brute-force도 나와있길래 개념도 적어둘 겸 정리하려고 한다.
Brute-force ?
brute-force는 우리말로 하면 '무식한 힘'으로 번역되며, 쉽게 말하면 완전탐색 알고리즘이다. 가능한 모든 경우의 수를 탐색한다는 특징을 가지고 있다. 그래서 만약 n개의 노드가 있다고 가정하면 총 경로의 개수는 (n - 2)! 가 나온다고 한다.
시간복잡도가 n!이 되면 너무너무 비효율적인 알고리즘이 되므로, 최단경로를 구할 땐 완전탐색은 지양하는 편이 좋을 거 같다.
이렇게 그래프와 최단경로에 대한 게시글도 마무리되었다. 다음 챕터에서는 알고리즘 수업 중 가장 재밌게 들었던 greedy approach를 다뤄볼 예정이다!
'알고리즘' 카테고리의 다른 글
| [알고리즘] CHAP 4. GA - Kruskal's algorithm (크루스칼 알고리즘) (0) | 2023.12.30 |
|---|---|
| [알고리즘] CHAP 4. The Greedy Approach (탐욕알고리즘) - Prim's alg (프림알고리즘) (4) | 2023.12.29 |
| [알고리즘] CHAP 2. Dynamic Programming (동적 프로그래밍) (1) | 2023.12.28 |
| [알고리즘] CHAP 1. Divide and Conquer (분할정복) - Master Theorem (1) | 2023.12.26 |
| [알고리즘] CHAP 1. Divide and Conquer (분할정복) - Quicksort (0) | 2023.12.26 |
