class 6
https://www.acmicpc.net/problem/2533
# 문제
페이스북, 트위터, 카카오톡과 같은 사회망 서비스(SNS)가 널리 사용됨에 따라, 사회망을 통하여 사람들이 어떻게 새로운 아이디어를 받아들이게 되는가를 이해하는 문제가 중요해졌다. 사회망에서 사람들의 친구 관계는 그래프로 표현할 수 있는데, 이 그래프에서 사람은 정점으로 표현되고, 두 정점을 잇는 에지는 두 정점으로 표현되는 두 사람이 서로 친구 관계임을 표현한다.
예를 들어, 철수와 영희, 철수와 만수, 영희와 순희가 서로 친구 관계라면 이를 표현하는 친구 관계 그래프는 다음과 같다.
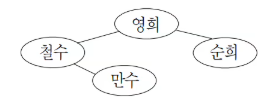
친구 관계 그래프를 이용하면 사회망 서비스에서 어떤 새로운 아이디어가 전파되는 과정을 이해하는데 도움을 줄 수 있다. 어떤 새로운 아이디어를 먼저 받아들인 사람을 얼리 아답터(early adaptor)라고 하는데, 사회망 서비스에 속한 사람들은 얼리 아답터이거나 얼리 아답터가 아니다. 얼리 아답터가 아닌 사람들은 자신의 모든 친구들이 얼리 아답터일 때만 이 아이디어를 받아들인다.
어떤 아이디어를 사회망 서비스에서 퍼뜨리고자 할 때, 가능한 한 최소의 수의 얼리 아답터를 확보하여 모든 사람이 이 아이디어를 받아들이게 하는 문제는 매우 중요하다.
일반적인 그래프에서 이 문제를 푸는 것이 매우 어렵다는 것이 알려져 있기 때문에, 친구 관계 그래프가 트리인 경우, 즉 모든 두 정점 사이에 이들을 잇는 경로가 존재하면서 사이클이 존재하지 않는 경우만 고려한다.
예를 들어, 8명의 사람으로 이루어진 다음 친구 관계 트리를 생각해보자. 2, 3, 4번 노드가 표현하는 사람들이 얼리 아답터라면, 얼리 아답터가 아닌 사람들은 자신의 모든 친구가 얼리 아답터이기 때문에 새로운 아이디어를 받아들인다.

친구 관계 트리가 주어졌을 때, 모든 개인이 새로운 아이디어를 수용하기 위하여 필요한 최소 얼리 어답터의 수를 구하는 프로그램을 작성하시오.
# 예제
입력 : 첫 번째 줄에는 친구 관계 트리의 정점 개수 N이 주어진다. 단, 2 ≤ N ≤ 1,000,000이며, 각 정점은 1부터 N까지 일련번호로 표현된다. 두 번째 줄부터 N-1개의 줄에는 각 줄마다 친구 관계 트리의 에지 (u, v)를 나타내는 두 정수 u와 v가 하나의 빈칸을 사이에 두고 주어진다.
8
1 2
1 3
1 4
2 5
2 6
4 7
4 8
출력 : 주어진 친구 관계 그래프에서 아이디어를 전파하는데 필요한 얼리 아답터의 최소 수를 하나의 정수로 출력한다.
3
# 필요개념
해당 문제에서 아이디어를 받아들일 수 있는 경우는 아래와 같다.
- 본인이 얼리 어답터일 때
- 친구들이 모두 얼리 어답터일 때
이 조건을 보고 너무 섣부르게 "그럼 친구가 많을 경우에는 본인이 얼리어답터인게 최소 어리어답터의 수를 구하는 길이겠다" 라고 판단해버려서 틀린 코드를 제출했다.
실제로 그런지 직접 따져보아야 하고, 따져보는 방법은 dp를 이용하는 것이다.
조건을 좀 더 자세히 들여다보면 아래와 같이 판단할 수 있다.
- 본인이 얼리어답터가 아니면 ?
- 내 친구들은 모두 얼리어답터여야만 한다.
- 본인이 얼리어답터라면?
- 내 친구들은 얼리어답터일수도, 아닐수도 ?
따라서 dp를 이용해 dp[ i ][ 0 ]은 본인이 얼리어답터가 아닐 경우 얼리어답터의 총 개수를, dp[ i ][ 1 ] 에는 본인이 얼리어답터일 경우 얼리어답터의 총 개수를 넣기로 했다. 마지막엔 둘 중 작은 값을 출력하면 된다.
트리구조에서 루트를 시작으로 쭉 내려와야 하기 때문에, dfs를 이용해 top-down 방식으로 배열을 채워갔다.

친구를 순회한 후 배열이 채워졌으면 채워진 배열을 이용해 parent 노드의 배열을 채운다.
dp[now][0] 은 본인이 얼리어답터가 아닐 경우이므로 -> 친구들이 얼리어답터인 경우만 더해준다.
dp[now][1] 은 본인이 얼리어답터일 경우이므로 -> 친구들의 여부는 크게 상관없다. 따라서 더 작은 값을 더한다.
이렇게 재귀와 dp를 이용해 문제풀이를 진행했다.
# Code
import java.io.*;
import java.util.*;
// 2533
public class Main {
static List<List<Integer>> lst = new ArrayList<>();
static boolean[] canInfo;
static int[][] dp;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
canInfo = new boolean[N + 1];
dp = new int[N + 1][2];
for (int i = 0 ; i <= N ; i++) {
lst.add(new ArrayList<>());
}
for (int i = 0 ; i < N - 1 ; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
lst.get(u).add(v);
lst.get(v).add(u);
}
dfs(1);
System.out.println(Math.min(dp[1][0], dp[1][1]));
}
private static void dfs(int now) {
canInfo[now] = true;
dp[now][1] = 1;
for (int child : lst.get(now)) {
if (!canInfo[child]) {
dfs(child);
dp[now][0] += dp[child][1];
dp[now][1] += Math.min(dp[child][0], dp[child][1]);
}
}
}
}
# 결과

'코딩테스트 > 백준 골드' 카테고리의 다른 글
| [백준] 1707: 이분 그래프 (DFS) - JAVA (1) | 2025.01.31 |
|---|---|
| [백준] 1520: 내리막길 (DFS, DP) - JAVA (1) | 2025.01.25 |
| [백준] 2357: 최솟값과 최댓값 (세그먼트 트리) - JAVA (0) | 2025.01.20 |
| [백준] 11054: 가장 긴 바이토닉 부분 수열 (DP) - JAVA (2) | 2025.01.17 |
| [백준] 2565: 전깃줄 (dp) - JAVA (1) | 2025.01.11 |
