728x90
반응형
이번 게시글은 탐욕 알고리즘의 마지막 알고리즘으로 다익스트라 알고리즘을 정리할 예정이다. 목차는 다음과 같다.
- Dijkstra's algorithm (다익스트라 알고리즘)
탐욕알고리즘은 아래 게시글에 설명되어있다.
https://wanna-developer02.tistory.com/51
[알고리즘] CHAP 4. The Greedy Approach (탐욕알고리즘) - Prim's alg (프림알고리즘)
이번 챕터에서는 탐욕알고리즘과 이를 이용하는 프림, 크루스칼, 다익스트라 알고리즘을 정리해보려고 한다. 한 게시물에 정리하기에는 내용이 너무 많아서 나눠서 정리할 예정이다. 목차는 다
wanna-developer02.tistory.com
1. Dijkstra 알고리즘
다익스트라 알고리즘은 가중치그래프에서 출발점으로부터 각 노드까지의 최단경로를 찾는 알고리즘이다. 특이하게 다익스트라알고리즘에서는 시작노드가 지정되어있다. 그래서 시작점에서 각 노드까지의 최단경로를 저장한다.
또 다른 특징은 한 번 방문된 정점의 D 원소값이 변하지 않는다는 것인데, 이러한 특징때문에 음수 가중치가 있을 때 무한루프에 걸리게 된다.
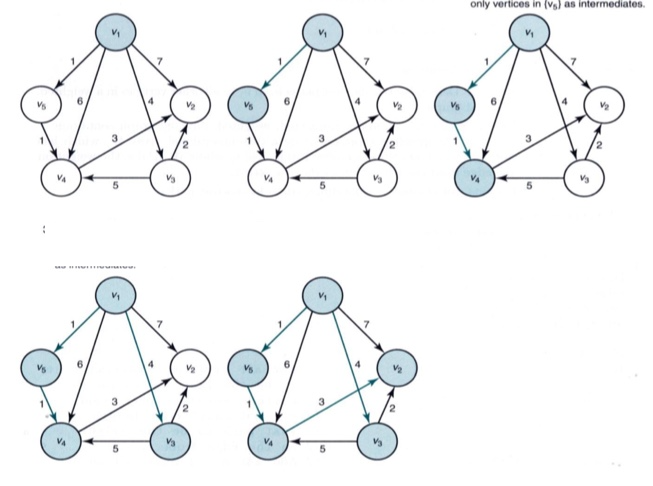
시작점은 v1이다!
# Code
visited = [False] * N
D = [sys.maxsize] * N
D[s] = 0
previous = [None] * N
previous[s] = s
for k in range(N) :
m = -1
min_val = sys.maxsize
for j in rnage(N) :
if not visited[j] and D[j] < min_val :
min_val = D[j]
m = j
visited[m] = True
for v, wt in list(g[m]) :
if not visited[v] :
if D[m] + wt < D[v] :
D[v] = D[m] + wt
previous[v] = m
시간복잡도는 프림과 동일하므로 생략할 예정이다! 다음 게시글에서는 Greedy Approach를 이용한 Knapsack Problem에 대해 정리할 예정이다!
'알고리즘' 카테고리의 다른 글
| [알고리즘] CHAP 6. Branch-and-Bound algorithm (분기한정 알고리즘) - 0/1 Knapsack 풀기 (2) | 2024.01.04 |
|---|---|
| [알고리즘] CHAP 5. Backtracking Algorithm (백트래킹 알고리즘) - Monte Carlo Algo- (1) | 2024.01.03 |
| [알고리즘] CHAP 4. GA - Kruskal's algorithm (크루스칼 알고리즘) (0) | 2023.12.30 |
| [알고리즘] CHAP 4. The Greedy Approach (탐욕알고리즘) - Prim's alg (프림알고리즘) (4) | 2023.12.29 |
| [알고리즘] CHAP 3. Graph Theory (그래프) - 그래프로 최단거리 구하기 (2) | 2023.12.28 |
