이번 챕터에서는 백트래킹 알고리즘에 대해 정리하려고 한다. 목차는 다음과 같다.
- Backtracking Algorithm (백트래킹)
- DFS
- BFS
- Monte Carlo Algorithm (몬테카를로 알고리즘)
- Solve problem
- 1. N Queens Problem
- 2. Sum-of-Subsets Problem
- 3. Graph Coloring Problem
- 4. Hamiltonian Circuits Problem
1. Backtracking Algorithm (백트래킹 알고리즘)
백트래킹 알고리즘은 어떤 조건을 가진 문제의 해결책을 찾기위해 탐색하는 알고리즘 중 하나이다. 모든 경우의 수를 탐색하긴 하지만, 완전탐색 알고리즘과 달리 어떤 조건을 가지고 있으므로 배제되는 경우들이 많아 효율이 더 높다. 가능성이 없는 노드를 발견하면 더이상 해당 노드를 탐색하지 않는 특징을 가진다.
이러한 특성 때문에 단순 반복문을 돌리는 것보다 효율이 더 높다!
이해가 힘들다면, 막다른 길을 만나면 다시 돌아가 새로운 길을 찾는 미로찾기를 생각하면 된다.
백트래킹의 구현은 보통 DFS나 BFS를 사용한다. (DFS를 더 많이 씀)
DFS
dfs는 Depth-First Search의 약자로 깊이우선탐색 알고리즘을 의미한다. 트리를 생각해보면 루트에서 시작하여 한개의 노드를 탐색하고 그 노드의 자식노드들을 먼저 탐색한다고 생각하면 된다.

# Code
visited = [None] * N // N은 노드개수
def dfs(v) :
visited[v] = True
for w in adj_lst[v] :
if not visited[w] :
dfs(w)
이렇게 재귀함수를 이용해 자식노드를 같은 방식으로 탐색한다.
이진트리가 아닌 그래프에서는 아래와 같은 순서로 탐색을 진행한다.

dfs만 하기 아쉬우니까 bfs도 설명하려고 한다!
+) BFS
bfs는 Breath-First Search의 약자로 너비우선탐색 알고리즘을 의미한다. dfs는 재귀로 자식노드를 먼저 탐색 했지만, bfs는 모든 이웃정점을 우선 방문하고, 그 노드들의 자식노드를 탐색하는 순서로 탐색한다.

# Code
visited = [None] * N
def bfs(i) :
queue = []
visited[i] = True
queue.append(i)
while len(queue) != 0 :
v = queue.pop(0)
for w in adj_list[v]:
if not visited[w] :
visited[w] = True
queue.append(w)
bfs는 큐를 이용하여 탐색한다! 이진트리가 아닌 그래프에서는 아래와 같이 탐색이 진행된다.

# Code
백트래킹 알고리즘은 DFS의 메소드와 비슷하게 탐색이 이루어진다. 아래 코드에서 promising은 조건을 만족했는지에 대한 여부이다.
void expand(node v) {
node u;
for (each child u of v)
if (promising(u))
if (there is a solution at u)
write the solution;
else
expand(u);
}
2. Monte Carlo Algorithm (몬테카를로 알고리즘)
몬테카를로 알고리즘을 이용해서 백트래킹 알고리즘의 효율성을 평가할 수 있다.
몬테카를로 알고리즘이란 무작위로 랜덤수를 생성한 후, 이를 기반으로 생성해서 구하고자 하는 정보의 확률을 계산하는 알고리즘이다. 난수 생성이 무한에 가까워질 경우 우리가 원하는 정보의 실제값으로 근사하다.
몬테카를로 알고리즘은 다음과 같은 특징이 있다.
- 실행되는 명령은 확률적 분포에 따라 랜덤으로 결정된다
- SST(State Space Tree)에서 같은 레벨의 모든 노드는 같은 promising function을 사용해야한다
- 같은 레벨의 노드는 children노드의 개수가 같아야한다
3. 해결할 수 있는 문제들
백트래킹으로 해결할 수 있는 문제들을 소개하려고 한다
1) N Queens Problem
이 문제는 N*N 체스보드에 4개의 queen을 올리는 문제이다. queen을 올릴 때 조건은 다음과 같다.
- 두 퀸은 같은 행에 있을 수 없다
- 두 퀸은 같은 열에 있을 수 없다
- 두 퀸은 같은 대각선에 있을 수 없다
이 점에 유의하여 퀸을 배치해야 한다.
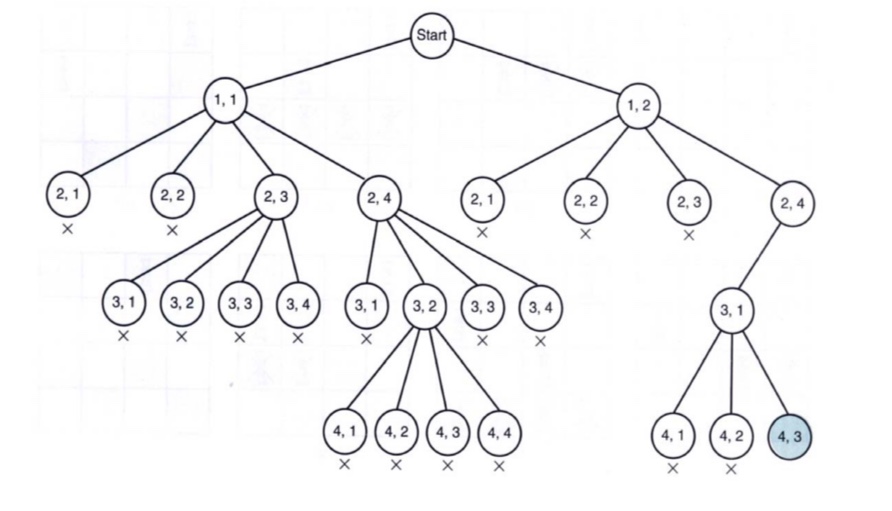
4-Queens 문제를 풀 때 state pace tree의 크기는 1 + 4 + 4^2 + 4^3 + 4^4 = 341이다. 이를 일반화하여 n-Queens라고 생각해보면 1 + n + n^2 + ... + n^n = (n^(n+1) - 1) / (n - 1) 로 쓸 수 있다. 하지만 이 경우에는 필요없는 연산이 정말 많다.
필요없는 연산을 빼면 N-Queen 문제를 다음처럼 쓸 수 있다.
1 + t0 + m0 t1 + m0 m1 t2 + ... + m0 m1 .. m(i-1) ti + ... 여기서 m0 < t0이다. m은 promising 함수에서 걸러진 노드를 뺀 것이다!
2) Sum-of-Subsets Problem
총 합을 미리 제시하고 (n) 노드의 합이 n인 sets을 찾는 문제이다. 이 문제에서 non-promising 한 경우는 다음과 같다.
- weight + w(i+1) > W인 경우 (W는 weight들의 총 합)
- weight + total < W인 경우
여기서 w(i+1)은 남은 노드 중 가장 가벼운 노드이다.

위 사진처럼 non-promising한 경우는 x표시를 하고 아예 탐색하지 않는 prune(가지치기) 작업을 하면 효율을 높일 수 있다.
3) Graph Coloring Problem
노드의 개수 n과 색의 개수 m이 주어지고, 무방향 그래프가 주어지고 그 중 edge들이 꼬일 일 없는 그래프인 planar 그래프로 주어진다.
주어진 것들을 이용해 최대 m개의 색으로 그래프에 색을 채우는 문제이다. 여기서 주의할 점은 인접한 그래프는 같은 색을 가질 수 없다는 점이다.
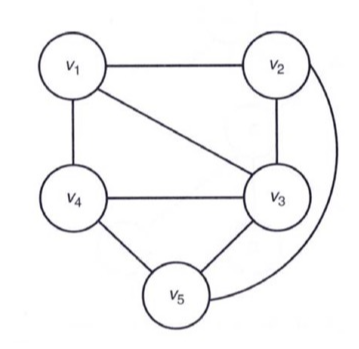

위 그래프에 색을 채우는 과정은 아래와 같이 state tree로 나타낼 수 있다. 참고로 아래 tree는 가지치기를 진행한 pruned state tree이다.

위 과정을 보면 m개의 색을 n번 넣어보므로 1 + m + m^2 + .. + m^n = (m^(n+1) - 1) / (m - 1) 로 쓸 수 있다.
4) Hamiltonian Circuits Problem
이 문제는 쉽게 설명하면 모든 노드를 단 한 번만 방문한 후 첫 노드로 돌아오는 문제이다. 여기서는 n개의 노드를 가진 무방향 그래프와 첫 노드가 무엇인지 주어진다.
이 문제의 경우 해결할 수 있는 그래프와 해결할 수 없는 그래프가 비교적 분명하게 나누어 질 것이다.
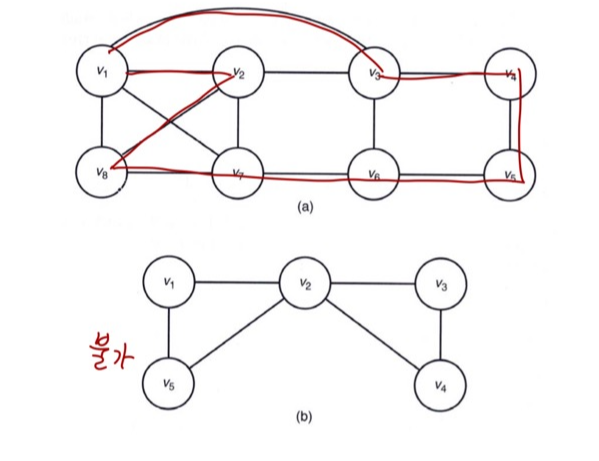
a는 돌아오는 것이 가능하지만, b는 노드 v2를 필연적으로 2번 지나칠 수밖에 없으므로 해결할 수 없다.
이 문제는 자기자신으로 돌아오는 건 불가능하므로 n-1개의 노드를 지나칠 수 있다. 그러므로 다음과 같이 쓸 수 있다.
1 + (n-1) + n-1)^2 + ... + ((n-1)^n - 1) / (n - 2)
이렇게 백트래킹 정리가 끝났다! 다음 챕터에서는 아마 Branch-and-Bound에 대해 정리할 것 같다
'알고리즘' 카테고리의 다른 글
| [알고리즘] CHAP 6. Branch-and-Bound algorithm (분기한정 알고리즘) - 0/1 Knapsack 풀기 (2) | 2024.01.04 |
|---|---|
| [알고리즘] CHAP 4. GA - Dijkstra's algorithm (다익스트라 알고리즘) (0) | 2023.12.30 |
| [알고리즘] CHAP 4. GA - Kruskal's algorithm (크루스칼 알고리즘) (0) | 2023.12.30 |
| [알고리즘] CHAP 4. The Greedy Approach (탐욕알고리즘) - Prim's alg (프림알고리즘) (4) | 2023.12.29 |
| [알고리즘] CHAP 3. Graph Theory (그래프) - 그래프로 최단거리 구하기 (2) | 2023.12.28 |
