class 4+
https://www.acmicpc.net/problem/2206
# 문제
N×M의 행렬로 표현되는 맵이 있다. 맵에서 0은 이동할 수 있는 곳을 나타내고, 1은 이동할 수 없는 벽이 있는 곳을 나타낸다. 당신은 (1, 1)에서 (N, M)의 위치까지 이동하려 하는데, 이때 최단 경로로 이동하려 한다. 최단경로는 맵에서 가장 적은 개수의 칸을 지나는 경로를 말하는데, 이때 시작하는 칸과 끝나는 칸도 포함해서 센다.
만약에 이동하는 도중에 한 개의 벽을 부수고 이동하는 것이 좀 더 경로가 짧아진다면, 벽을 한 개 까지 부수고 이동하여도 된다.
한 칸에서 이동할 수 있는 칸은 상하좌우로 인접한 칸이다.
맵이 주어졌을 때, 최단 경로를 구해 내는 프로그램을 작성하시오.
# 예제
입력 : 첫째 줄에 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 1,000)이 주어진다. 다음 N개의 줄에 M개의 숫자로 맵이 주어진다. (1, 1)과 (N, M)은 항상 0이라고 가정하자
6 4
0100
1110
1000
0000
0111
0000
출력 : 첫째 줄에 최단 거리를 출력한다. 불가능할 때는 -1을 출력한다.
15
# 필요개념
처음에 문제를 접했을 때, dfs로 구현을 했었는데 시간초과로 실패해서 bfs로 접근했다. 이 문제는 단순히 최단경로를 탐색하는 것이 아니고, 벽을 한 번 부술 수 있음에 유의해야 한다. 벽을 부순 경우가 더 빠를 수도 있고 그냥 가는게 빠를 수도 있기 때문에 이 두가지 경우 방문여부 체크를 별도로 진행해야 한다. 이차원배열 두개를 만들어도 되지만, 나는 삼차원배열을 생성해주었다.
[ ][ ][ 0 ] 은 벽을 부순적 없는 경우의 방문여부 체크 배열이고, [ ][ ][ 1 ] 은 벽을 부순 적 있는 경우의 방문 여부 체크 배열이다.
✅ 벽을 부수고 온 케이스들은 벽이 아닌 곳만 지나갈 수 있다. 따라서 아래와 같이 코드를 작성했다.
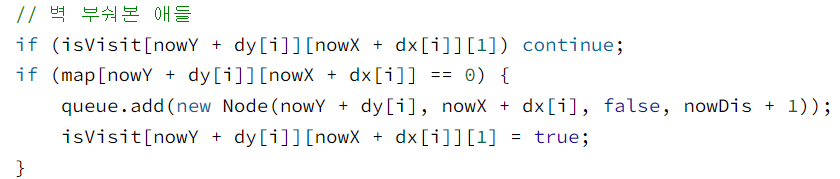
✅ 벽을 부수지 않고 온 케이스는 벽인 곳도 지나갈 수 있다.
- 벽을 만난 경우 : 부술 수 있는 기회를 날려주고, 벽을 부순 방문여부 배열에 반영한다.
- 벽을 만나지 않은 경우 : 벽을 부수지 않은 배열에 반영한다.

# Code
import java.io.*;
import java.util.*;
public class Main {
static int[][] map;
static boolean[][][] isVisit;
static int[] dx = {1, 0, -1, 0}; // 동 남 서 북
static int[] dy = {0, 1, 0, -1};
static int N;
static int M;
static int sol = Integer.MAX_VALUE;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
map = new int[N + 1][M + 1];
isVisit = new boolean[N + 1][M + 1][2];
for (int i = 1 ; i <= N ; i++) {
String s = br.readLine();
for (int j = 1 ; j <= M ; j++) {
map[i][j] = Integer.parseInt(String.valueOf(s.charAt(j - 1)));
}
}
bfs(1, 1, 1);
if (sol == Integer.MAX_VALUE) sol = -1;
System.out.println(sol);
}
private static void bfs(int y, int x, int chance) {
Queue<Node> queue = new ArrayDeque<>();
queue.add(new Node(y, x, true, 1));
while (!queue.isEmpty()) {
Node now = queue.poll();
int nowY = now.y;
int nowX = now.x;
boolean nowChance = now.chance;
int nowDis = now.distance;
// System.out.println("y : " + nowY + " x : " + nowX + " / chane : " + nowChance + " / dis : " + nowDis);
if (nowY == N && nowX == M) {
sol = Math.min(sol, nowDis);
return;
}
for (int i = 0 ; i < 4 ; i++) {
if (canGo(nowY + dy[i], nowX + dx[i])) {
if (nowChance) {
if (isVisit[nowY + dy[i]][nowX + dx[i]][0]) continue;
// 벽 안 부숴본 애들
if (map[nowY + dy[i]][nowX + dx[i]] == 1) {
queue.add(new Node(nowY + dy[i], nowX + dx[i], false, nowDis + 1));
isVisit[nowY + dy[i]][nowX + dx[i]][1] = true;
} else {
queue.add(new Node(nowY + dy[i], nowX + dx[i], true, nowDis + 1));
isVisit[nowY + dy[i]][nowX + dx[i]][0] = true;
}
} else {
// 벽 부숴본 애들
if (isVisit[nowY + dy[i]][nowX + dx[i]][1]) continue;
if (map[nowY + dy[i]][nowX + dx[i]] == 0) {
queue.add(new Node(nowY + dy[i], nowX + dx[i], false, nowDis + 1));
isVisit[nowY + dy[i]][nowX + dx[i]][1] = true;
}
}
}
}
}
}
private static boolean canGo(int y, int x) {
return y > 0 && x > 0 && y <= N && x <= M;
}
}
class Node {
int y;
int x;
boolean chance;
int distance;
public Node(int y, int x, boolean chance, int distance) {
this.y = y;
this.x = x;
this.chance = chance;
this.distance = distance;
}
}
# 결과

'코딩테스트 > 백준 골드' 카테고리의 다른 글
| [백준] 1197: 최소 스패닝 트리 (MST, 크루스칼 알고리즘) - JAVA (0) | 2024.10.24 |
|---|---|
| [백준] 다각형의 면적 (신발끈 공식, 기하학) - JAVA (2) | 2024.10.21 |
| [백준] 1967: 트리의 지름 (DFS) - JAVA (2) | 2024.10.13 |
| [백준] 1753: 최단경로 (다익스트라 알고리즘) - JAVA (1) | 2024.10.10 |
| [백준] 1504: 특정한 최단경로 (다익스트라 알고리즘) - JAVA (0) | 2024.10.05 |
